І. Організаційний момент.
Добрий день, діти. Сьогодні я бажаю вам бути (слайд 1)
Уважними
Сміливими
Працелюбними
Ініціативними
Хоробрими
Тобто, одним словом, - успіху!
ІІ. Актуалізація опорних знань.
1) Сьогодні на уроці ми продовжимо вивчення однієї з найцікавіших тем математики
– «Погресії». Їх внутрішня гармонія, строга витончена краса роблять теорію
прогресій відображенням властивостей об’єктивного світу, що існує незалежно
від нас, нашої свідомості.
Слово «прогресія» латинського походження «progression» і означає «рух уперед»
( як і слово «прогрес»). То ж зараз за допомогою тестування з’ясуємо, чи готові
ми рухатись уперед на шляху нашого розвитку. Знайдіть на робочих столах ваших ноутбуків
тест «Геометрична прогресія» та пройдіть його. Отримані результати занесіть в листок
самоконтролю.
Учні протягом 8 хв. проходять тестування(слайд2)за персональними комп’ютерами.
Тести складені за допомогою програми MyTest.
2) Працюючи із тестами, які означення, формули ви використовували? (Учні дають
відповіді)
Добре, але крім них нам сьогодні потрібно пригадати і арифметичну прогресію. Тому
давайте встановимо відповідність між твердженнями та відповідними формулами.
(слайд 3)

ІІІ. Повідомлення теми, мети. Мотивація навчання.
Як сказав М.І.Лобачевський (Слайд 4)
«Немає жодної галузі математики, якою б абстрактною вона не була,
котра коли-небудь не виявиться застосовною до явищ дійсного світу» .
Тобто, немає теорії без практики , тому темою нашого уроку є «Розв’язування
задач». (слайд 5 )
Виходячи з теми, як би ви визначили мету нашого уроку? (Учні визначають мету)
.
Тож можна в такий спосіб підсумувати сказане вами:
Мета уроку: (слайд 6)
- Показати застосування геометричної прогресії у прикладних задачах;
- Поглибити вміння розв’язувати задачі на прогресії.
IV. Захист проектів.
Вчитель: Ще на початку вивчення теми ви отримали завдання
підготувати міні-проекти про зв'язок геометричної прогресії із різними
науками. Ми вже з’ясували, який зв'язок існує між геометричною прогресією і
легендами про виникнення шахів та про винагороду Теренція, за допомогою чого здійснюється
поділ нейтронів під час ядерної ланцюгової реакції.
Сьогодні ж ми заслухаємо спікерів ще двох груп, а інші продовжать на наступному
уроці. Наданий вами матеріал для захисту я включила в презентацію до нашого сьогоднішнього
уроку.
Тож зараз надамо слово Біологам.
Спікер біологів. (слайд 7) В біології
прогресії пов’язані з такими темами, як розмноження, поділ клітин, та інші. Неможливо
розв’язати біологічні задачі з даних тем, не використавши знання про прогресії.
За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються
прогресивно або регресивно.
Пропонуємо вашій увазі наступні задачі:
1. За геометричною прогресією розмножується мак. Відомо, що головка маку містить
3000 зернят. Скільки квіток зійде на 5-й рік, якщо вважати, що зійде кожна насінина?
Цікаво! Приблизно 243×1015 квіток! Вони б зайняли площу, яка у 2000
разів перевищує площу земної поверхні.
2. Уявімо, що на початку нашої ери жінка М народила дві доньки, кожна з них до
30 років народила теж дві доньки і т.д. Чи можливо це? Скільки б за таких умов нащадків
М жило б у наш час?
Це близько 7∙1019, що значно перевищує кількість людей на планеті.
Тому це не можливо.
3. Задача брудних рук. Бактерія, потрапивши в організм людини, до
кінця 20-ї хвилини ділиться на 2, кожна з них через 20 хв ще на дві і т.д. Скільки
бактерій стане в організмі людини через добу?
Розв’язання.
1доба=24год.; 24год.=1440хв.; 1440:20=72
За умовою задачі отримаємо геометричну прогресію: 1;2;4;8;…;
b1=1,
q=2
Sn=((b1(qn-1)):q-1)=((1*(272 -1)):1)= 272 - 1≈
272(бактерії)
Відповідь: в організмі за добу буде 272 бактерій.
Вчитель: Можете уявити собі, що
робиться в вашому організмі через добу! Ця задача закликає вас не нехтувати правилами
власної гігієни.
Дякуємо біологам і надаємо слово Фінансистам.
Спікер фінансистів. (Слайди 8,9) Працюючи над проектом,
ми з’ясували, що за законом геометричної прогресії зростає розмір вкладу в
ощадбанку, також з поняттям геометричної прогресії пов’язане поняття ануїтету. Геометрична
прогресія лежить в основі діяльності різноманітних фінансових пірамід.
Вашій увазі ми пропонуємо такі задачі:
1. Ви хочете взяти в банку кредит на 2000 грн. Умови кредитування:
за 1день вам нараховують 1 коп.; за 2 день - 2 коп.; за 3 день – 4 коп.; за
4 день - 8 коп. і т.д. Чи уклали б ви договір з цим банком, не менше
ніж на 30 днів?
Зрозуміло, що ні. Бо вже через 11 днів сума нарахувань перевищить отриманий кредит.
2. Старовинна задача. Купівля коня.
Дехто продавав коня за 156 рублів, але покупець передумав
купувати коня і повернув його продавцю зі словами: «Немає мені інтересу купувати
за таку ціну коня, який таких грошей не коштує». Тоді продавець запропонував
інші умови: «Якщо по-твоєму ціна коня висока, то купи лише цвяхи з його підков,
коня одержиш тоді на додачу безкоштовно. Цвяхів у кожній підкові 6. За перший цвях
дай мені всього ¼ копійки, за другий – ½ копійки, за третій – 1 копійку і т.д.»
Покупець, бажаючи задарма одержати коня, погодився. За яку суму він придбав коня?
Відповідь: 4 194 300 ¾ коп..
Вчитель. Так, за таких умов можна дати і коня на додачу.
Дякуємо фінансистам, а спікерам тих груп, що залишились, ми надамо слово на наступних
уроках.
V. Поглиблення знань.
(слайд 10) А як сказав відомий математик Д. Пойа: «Якщо ви хочете навчитися
плавати, то сміливо заходьте в воду, а якщо хочете навчитися розв’язувати задачі,
то розв’язуйте їх».
Розв’яжемо наступні задачі.
Робота з підручником.(слайд 11)
№ 35.42∙∙. Знайдіть чотири числа, з яких перші три
складають геометричну прогресію, а останні три – арифметичну, причому сума крайніх
чисел дорівнює 14, а сума середніх дорівнює 12.
Розв’язання.
Нехай
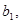
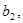
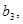
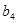 - дані числа. Тоді
- дані числа. Тоді
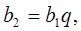
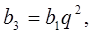
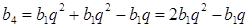 .
.
За умовою задачі складемо і розв’яжемо систему рівнянь:
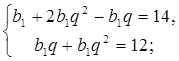
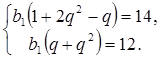 <
<
Оскільки
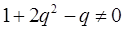 , поділивши
друге рівняння на перше, отримаємо рівняння
, поділивши
друге рівняння на перше, отримаємо рівняння
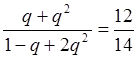 , яке рівносильне
рівнянню
, яке рівносильне
рівнянню
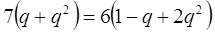 ,
,
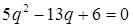 ,
,
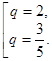
Якщо
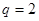 , то
, то
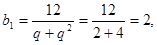
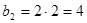 ,
,
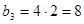 ,
,
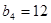 .
.
Якщо
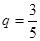 ,
то
,
то
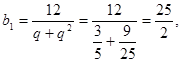
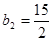 ,
,
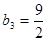 ,
,
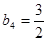 .
.
Відповідь: 2, 4, 8, 12 або
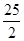 ,
,
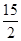 ,
,
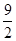 ,
,
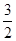 .
.
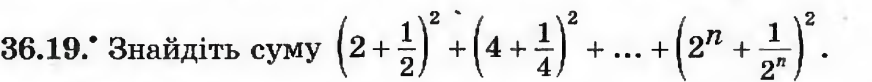
Один учень обчислює суму 4+16+…+2n,
другий - суму ¼+1/16+…+1/2n. Дома учні закінчують знаходження заданої в умові суми.
Відповідь:
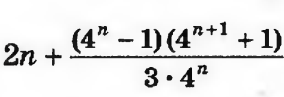 .
.
№ 36.20∙∙. Знайдіть кількість членів скінченної геометричної
прогресії, знаменник якої
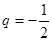 , перший член
, перший член
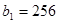 , а сума всіх
членів
, а сума всіх
членів
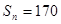 <.
<.
Розв’язання.
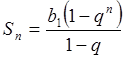 ,
тоді за умовою задачі складемо і розв’яжемо рівняння:
,
тоді за умовою задачі складемо і розв’яжемо рівняння:
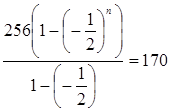 ,
,
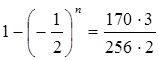 ,
,
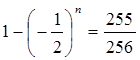 ,
,
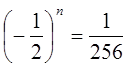 ,
,
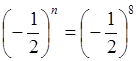 ,
,
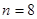 .
.
Відповідь: 8.
Вчитель: Коли ми з вами шукали суму n перших членів арифметичної прогресії, ми використовували
різні формули, для геометричної прогресії ми ж використовуємо одну формулу. Чи означає
це, що інших формул не існує?
Я пропоную вам розв’язати №36.22. До речі, в дещо іншому формулюванні ця задача
наводиться в конкурсних збірниках для підготовки до вступу у вищі навчальні заклади.
№ 36.22∙∙. Нехай
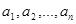 - послідовні
члени геометричної прогресії,
- послідовні
члени геометричної прогресії,
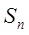 - сума її
- сума її
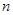 перших
членів. Доведіть, що
перших
членів. Доведіть, що
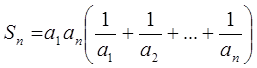 .
.
Доведення.
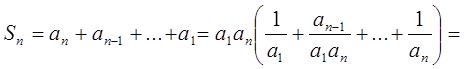
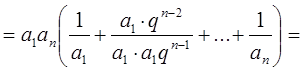
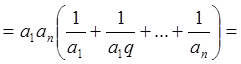
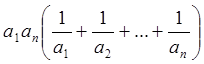 , що й потрібно
було довести.
, що й потрібно
було довести.
Вчитель. Отже, ми отримали ще одну формулу для обчислення
суми
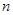 перших
членів геометричної прогресії. Дома ви спробуєте застосувати її до розв’язування
№ 36.23.
перших
членів геометричної прогресії. Дома ви спробуєте застосувати її до розв’язування
№ 36.23.
VI. Підсумок уроку. (слайд 12)
Рефлексія.
Сьогодні на уроці я
дізнався...
зрозумів...
навчався...
найбільший мій успіх – це...
на наступному уроці я хочу...
VII. Завдання додому
(слайд 13)
1) №36.23, 36.21
№ 36.23*. Знайдіть добуток 100 перших членів геометричної
прогресії
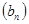 , якщо
, якщо
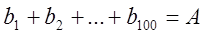 ,
,
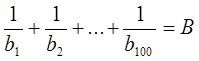 .
.
Розв’язання.
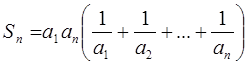 .
.
Тоді
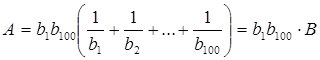 , звідси
<
, звідси
<
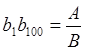 .
.
За властивістю геометричної прогресії
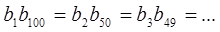 .
.
Тоді
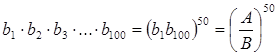 .
.
Відповідь:
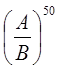 .
.
№ 36.21
Знайдіть кількість членів скінченної геометричної прогресії, знаменник якої
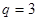 , останній
член
, останній
член
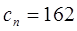 , а сума всіх
членів
, а сума всіх
членів
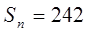 .
.
Розв’язання.
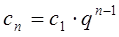 ,
,
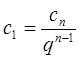 .
.
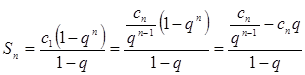 .
.
За умовою задачі складемо і розв’яжемо рівняння:
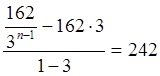 ,
,
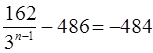 ,
,
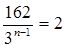 ,
,
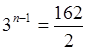 ,
,
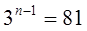 ,
,
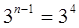 ,
,
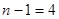 ,
,
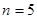 .
.
Відповідь: 5.
2) Довготривале домашнє завдання.
До закінчення вивчення теми розв’язати розрахункову роботу.
Розрахункова робота на сайті: https://sites.google.com/site/star2matem/
